More a journal than an educational treatise, Math from Three to Seven chronicles the uniquely soviet phenomenon known as Математические Кружки (Math Circles), applied specifically to young kids. I personally experienced a version of this growing up in Vancouver courtesy of my parent's Компания (a tight-knit friend-group) where various uncles and aunts DP, AL, GJ, YX, MS, and others took to supplementing the education of the next generation. DP led the math circle, and I, having had the least soviet schooling, really struggled compared to my peers. It was revealing and humbling and formative. DP's circle was more formal and rigorous since we were older, but Zvonkin's circles remind me a lot of that experience.

Reflecting on the concept of Subject Circles, it strikes me as a rare and great example of civic society in Russian culture. In fact, these band-scale groups of ~10 families are very strong in Russian culture. Could it be that civic society there is set up for much smaller groups than in the west?

Ok philosophical musings aside, this book is quite tactical and stays close to the straight and narrow. Most of his energies are spent on chronicling his successes and failures teaching mathematics to groups of young children, with an emphasis not on getting to the answer, but on asking interesting questions:

It is not the puzzles, nor their solutions, that are interesting, but the process, the path that connects them. [...] What is the point of my lessons? It’s fun to ask questions and look for answers. It’s a way of life.

Rarely does Zvonkin digress into philosophy or development psychology, and when he does he cites awesome stuff, some of which is heartwarmingly familiar, such as Mindstorms by Seymour Papert. Like language, mathematics is acquired naturally, not through rigorous and systematic approaches.

The best way to learn french is to grow up in France. The best way to learn math is to grow up in Mathland. - Seymour Papert

My main takeaway from the book is a list of inspiring “problems” to show my own kids aged four and seven, to cultivate their mathematical curiosity.

Problems to cultivate curiosity

Explore a Möbius strip. Make one regular ring, and one as a Möbius strip. See how drawing a line down the middle works in both cases. See what cutting down that line does in both cases.

Draw and define quadrilaterals and sneak in some basic set ideas. Maybe a Venn diagram too. Explain squares, rectangles, trapezoids, parallelograms. How many of which are there? What can we say about rules here?

Talk about fantastical situations and discuss transitivity. For example imagine an ant is bigger than a dog and a dog is bigger than an elephant. Then what do we know about ants and elephants? This relies on Smedslund's work on idea conflict: when individuals encounter contradictory ideas, particularly in social contexts, they are more likely to engage in reflection and actively seek to resolve the conflict, leading to cognitive growth.

Partial ordering of clothes. In what order do you put on clothes? What order do you take them off? Note you can put on your hat first, or your socks first, but there are dependencies when it comes to shoes.

In the same vein as clothes, a structure made out of blocks also has a partial ordering. Can kids create a dependency graph for constructing the structure? I found this PERT graph idea really neat:

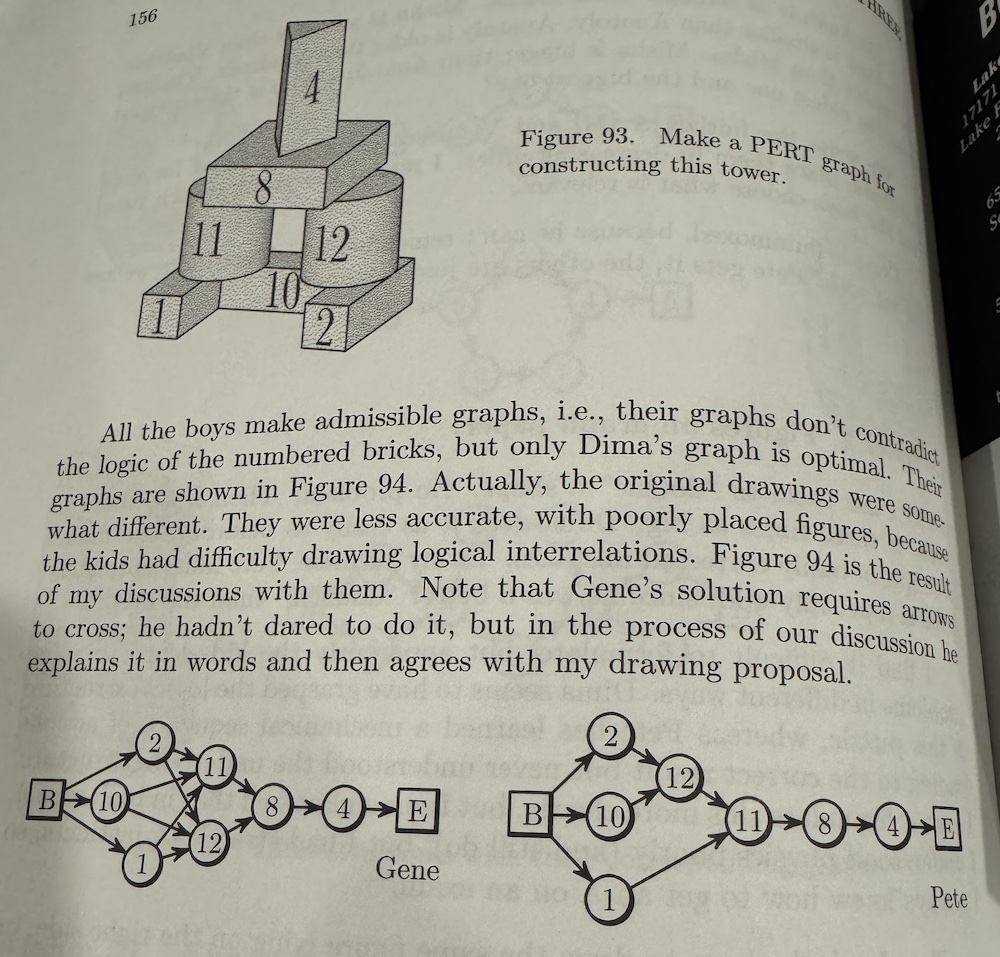
Five choose two: Zvonkin spent quite a bit of time with his circles trying to approach the same combinatoric problem from many different perspectives, all isomorphic to one another. But let the kids figure out that all of these problems are the same organically. 1. Color in chains of length five made out of red and blue links. How many chains are there? 2. Get five bins and two balls. How many ways are there to place the balls in these bins? 3. How many paths are there from one corner of a 5x2 rectangle to the other? Do this on graph paper. Encode each path as a sequence of Right (R) and Up (U) steps.

Rectangle counting: how many rectangles are there in a rectangle with a split in the middle? In a grid of 2x2 squares.

Frequency analysis for which sum of two dice rolls is the most common? Try it out. Make a table ourselves, then count how frequent each roll is. See if we can make bets!

Prime numbers through geometry. Try to make a rectangle out of N cubes. Can you do it with 9? Can you do it with 12? In how many ways? Try with 19. Do it systematically for all numbers up to say 28, making a table of primes and composites.

Patronymics is a fun puzzle. But less relevant in an Anglo setting. Still a cool formula: write out an empty family tree and then provide a set of names and patronyms. Arrange the people into the family tree.

Graph paper games for nerds. I draw something on a graph paper, and then get the kids copy it. Then have them rotate it by 90 degrees. Flip it. Scale it up. In another variant, I draw a pattern on a graph paper and get the kids to continue the pattern.

Three utilities problem: A little bit of graph theory with 3 houses and 3 wells. Can you make a path from each house to each well without having any paths cross?

Homeomorphic letters: imagine letters made out of bendable wire which can be compressed squished etc. Classify them into categories of homeomorphisms. Here's a paper with more detail.

Gauss Summation: see if I can tease the idea for getting a closed form solution for adding the first N numbers! This is a problem that Gauss solved as a child with the doubling backwards trick. What a great clean proof, still can't get over it decades later.

Draw water levels: Try the water level game with Eliana and Zyam. See if they can draw the water line on a drawing of a tilted water bottle.

Books and pointers to check out:

• Hailstone numbers: $U_{n+1} = u_n/2$ if $U_n$ is even and $U_{n+1} = 3 U_n$ otherwise. The Collatz conjecture says this sequence converges to 1 but remains unproven.
• Frames Of Mind: The Theory Of Multiple Intelligences by Howard Gardner