Book of Why came up as part of a reading group I'm involved in. I recommend this book only reluctantly. In the end, Pearl convinced me that causal inference is important and historically under-appreciated. Science progresses as a step function, and I think that in the current step in AI (deep learning) we are already starting to see the plateau.

My reluctance stems mainly from the way the material is presented. The book is a strange combination of anecdotes, verbal descriptions that genuinely help build intuition, some case studies, and a bunch of name dropping of students and collaborators. Most of it appears to be written for a popular audience, but sometimes the author jumps into mathematical formulas seemingly conjured from mid-air with very little explanation. Other times he provides terse proofs that read more like a math text book than anything else. Overall, the book is not well structured and awkwardly straddles the line between popular science, textbook, and paper. I was also annoyed by the aggrandizing use of "Causal Revolution", which I think detracted from its credibility.

Some chapters were especially tough, in particular Chapter 9, nominally about mediation, seemed to drag on pointlessly. I also found some parts challenging to internalize, particularly the front- and back-door criterion: what they are for, and what they allow you to do. Perhaps if I was actively studying statistics, and had more time to delve deeper into the content, I would be more patient with the author, and find more time to work out the details of the mathematics in my spare time. I think an interactive explanation of a causal diagram, data set and application of one of the de-confounding criterion would be super instructive. Nonetheless, here are the Pearls I managed to uncover for myself:

Ladder of causation: Early on, the author presents "three distinct levels of cognitive ability: seeing, doing, and imagining.":

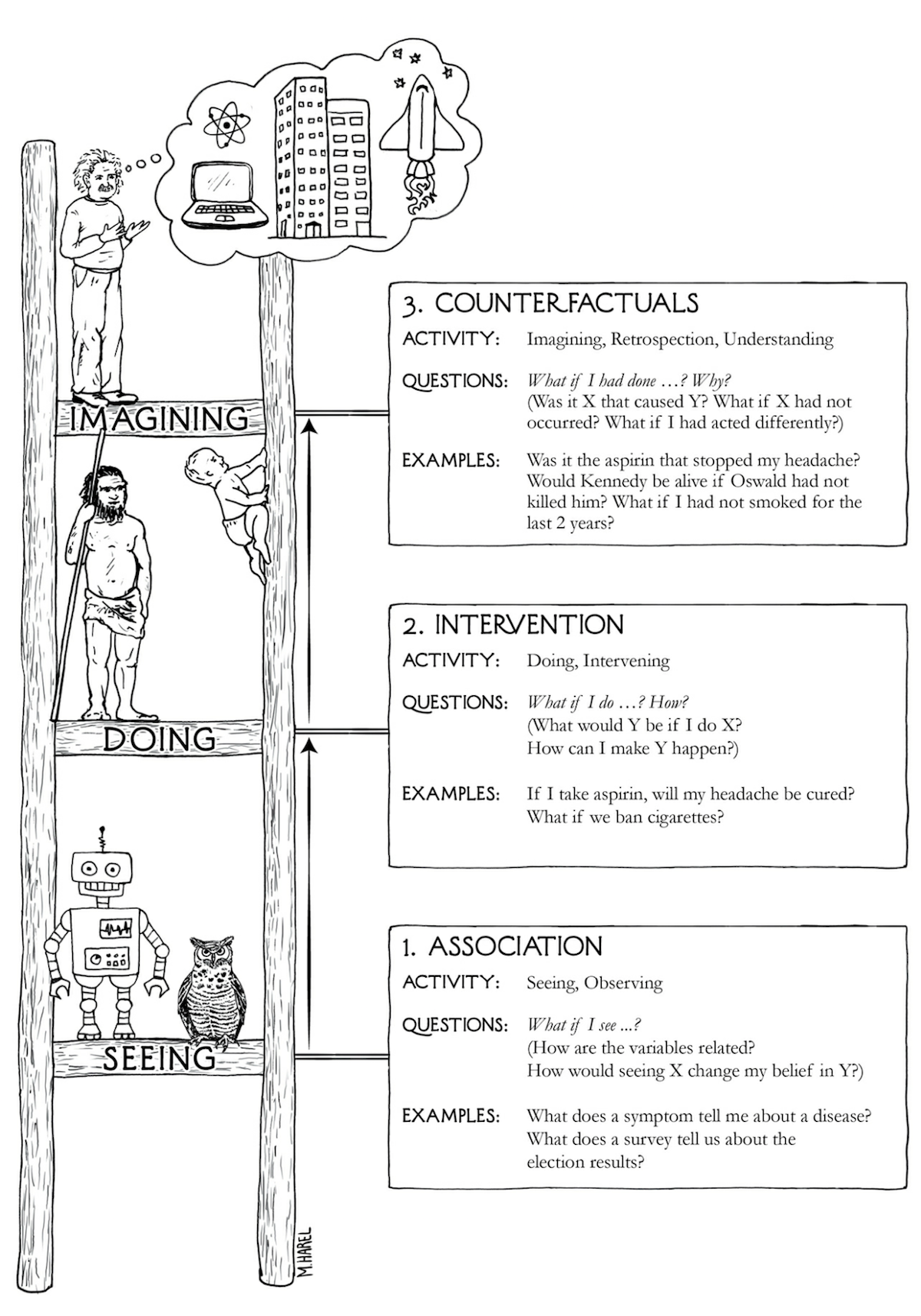
The vast majority of today's machine learning resides on the first rung of the ladder: observational data. Pearl believes that the core of human intelligence resides on higher rungs: "Deep learning has given us machines with truly impressive abilities but no intelligence." Later, he suggests this more explicitly: "I conjecture, that human intuition is organized around causal, not statistical, relations." This jives well with my intuition.

Beyond RCTs: what made me most interested in this book is the idea that causality can be established by means other than randomized control trials (RCTs). Pearl suggests having more than just data, but also a causal model, in the form of a directed acyclic graph (DAG), originally introduced by Sewall Wright. Pearl really pushes on this, evangelizing the concept. "A sufficiently strong and accurate causal model can allow us to use rung-one (observational) data to answer rung-two (interventional) queries." In many cases, running an RCT may be physically impossible (eg. can't make people become obese to study the effect of obesity on heart disease), or unethical (eg. can't force random people to smoke for 10 years).

However it’s unclear to me how one is to generate the causal model in the first place, and how you to ascertain that the model is "string and accurate". Pearl says so himself: "If she is confident that her causal model accounts for a sufficient number of deconfounders and she has gathered data on them, then she can estimate the effect of Fertilizer on Yield in an unbiased way." That's a fair amount of hedging.

Blending probability and logic: Although he never states it explicitly, Pearl's causal graphs seem to bridge the gap between formal logic (eg. A implies B) with probability. This is interesting, but I think Pearl is very much a statistician, since he hardly ever mentions logic, only introducing concept of necessary and sufficient towards the end of the book.

Casual aversion in stats: Pearl spends a lot of time complaining about the mantra "correlation does not imply causation" embodied by various authoritarian statisticians like Karl Pearson, and R. A. Fisher. Instead of such a strong statement, the author proposes "some correlations do imply causation," although he does dial it back and suggests that it may instead be called "provisional causality".

Causal diagrams: The path diagram concept introduced by Wright was met with resistance by his contemporaries, who were drawn to the allure of just looking at the data without any models, since the data is objective, and models are subjective. This is where Bayesian Statistics comes in, which tells you how to update Beliefs based on Evidence.

Disease prevention: James Lind discovered that citrus fruits prevent scurvy. John Snow (not that one) discovered that water contaminated with feces causes cholera. These findings were based on observational data, before widespread use of RCTs, yet causation was established.

Judicious biblical references: I loved that Pearl often cited the Bible in this book, most prominently the example of a controlled experiment from the Book of Daniel, but also chapter heading quotes from the Book of Jonah: "At last the sailors said to each other, Come and let us cast lots to find out who is to blame for this ordeal.", and Maimonides: "All is pre-determined, yet permission is always granted." (Really makes me want to read Nevi'im and Ketuvim one day.)

Monty Hall problem: In Chapter 6, the book meanders onto the topic of paradoxes, which is a bit of a tangent, but I guess is intended to illustrate the limitations of "first-rung" intuitions, and ways in which causal thinking can nullify these supposed paradoxes. Imagine a game show where contestants pick one of three doors, one of which has a car behind it, and two of which have goats. When the contestant opens one door, the host will pick one with a goat. The host will then open another door for the contestant. Should the contestant switch doors? The answer is yes.

Finally I understood it like this: by the rules of the game, the host (who knows where the goats and cars are) must open a door to reveal a goat. By so doing, he has revealed information about the door you picked. (This was made clear in the Bayesian explanation, without any reference to causality.)

Simpson's paradox: Imagine a drug that is supposed to reduce the risk of a heart attack. Here's fictional data for such a scenario:

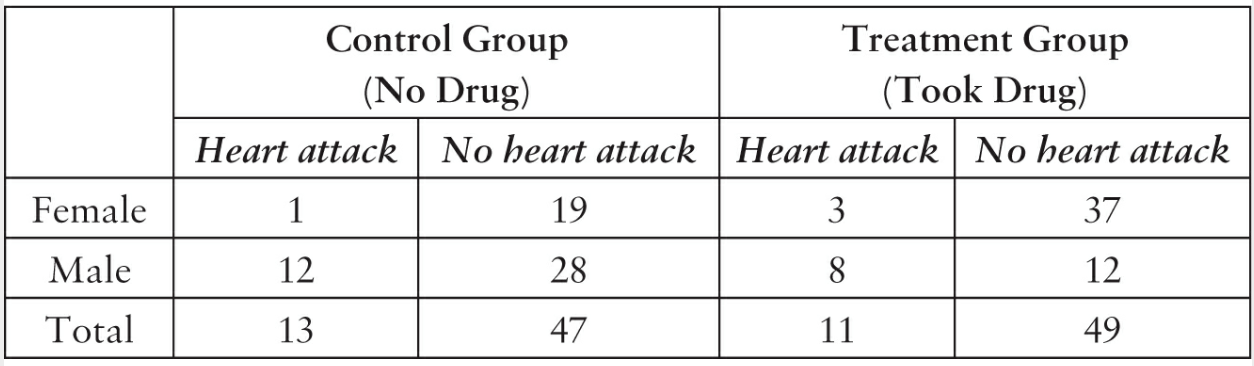
From the data, this drug has a negative effect on men (30% without, 40% with drug), a negative effect on women (5% without, 7.5% with), but overall better (22% without, 18% with). This doesn't make sense: logically, either the drug increases heart attacks for people, or the opposite. It's a question of partitioning vs. aggregating the data. Pearl's fictional example is resolved by the fact that gender affects whether or not you take the drug in the first place. Women had a preference for taking the drug, and men had the opposite preference, so you would need to control for gender.

Here's a visual example I found approachable. Both illustrations show the same data set, in one case aggregated and in another case partitioned by age.

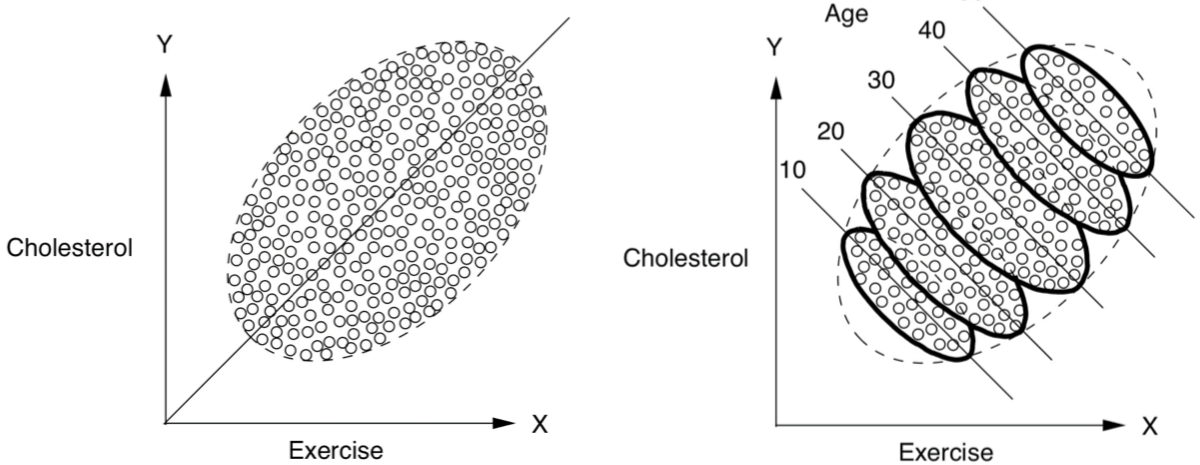
In the graphical example above, the more you age, the more they exercise. If you don't control for age it, it appears that the more you exercise, the higher your cholesterol! To be clear, by partitioning the group by age, you control for age and get to see the relationship which is muddied in aggregate.

Causal diagrams tell you what to control for

A whole chapter of the book is dedicated to the smoking and cancer debate of the mid-20th century. Many statisticians were highly skeptical of the causal argument. Some lurking third factor could be the cause, such as a gene that causes people to both crave cigarettes and made them more likely to develop lung cancer. In causal diagram form, the debate is between these two scenarios:

Junctions: every causal diagram consists entirely of these three types of junctions:

1. A → B → C: Mediator junction. Example: Fire → Smoke → Alarm. Fire causes the Smoke, and Smoke triggers the Alarm.
2. A ← B → C: Fork junction. Example: Shoe Size ← Age of Child → Reading Ability. Children with larger shoe sizes tend to read better, but it's not a causal relationship.
3. A → B ← C : Collider junction. Example: Talent → Celebrity ← Beauty. Suppose only one of talent and beauty is sufficient to be a celebrity. Then, if a celebrity were a good actor, they would need to be less beautiful. Conversely, if they were beautiful, they would need to be less talented.

Controlling for junctions: if you view a causal diagram as pipes conveying information from a starting point to an ending point, each type of junction can be blocked by controlling for a certain variable:

1. In a mediator (A → B → C) or fork (A ← B → C) the pipe between A and C is open, but controlling for B closes the pipe.
2. In a collider (A → B ← C), the pipe between A and C is closed, but controlling for B opens the pipe.

Back-door adjustment: Shit I really don't get it. This book doesn't do a great job of explaining the technical parts. I'll pause for now, and try approaching the material with this course instead: https://www.coursera.org/learn/crash-course-in-causality/home/welcome.